Privacy Canada is community-supported. We may earn a commission when make a purchase through one of our links. Learn more.
Caesar Cipher
The Caesar Cipher, also known as a shift cipher, is one of the oldest and simplest forms of encrypting a message.
It is a type of substitution cipher where each letter in the original message (which in cryptography is called the plaintext) is replaced with a letter corresponding to a certain number of letters shifted up or down in the alphabet.
For each letter of the alphabet, you would take its position in the alphabet, say 3 for the letter ‘C’, and shift it by the key number. If we had a key of +3, that ‘C’ would be shifted down to an ‘F’ – and that same process would be applied to every letter in the plaintext.
In this way, a message that initially was quite readable, ends up in a form that cannot be understood at a simple glance.
For example, here’s the Caesar Cipher encryption of a full message, using a left shift of 3.

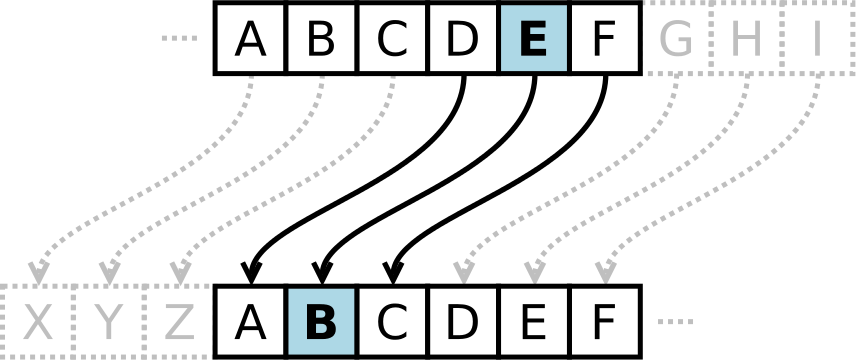
As unreadable as the resulting ciphertext may appear, the Caesar Cipher is one of the weakest forms of encryption one can employ for the following reasons:
- The key space is very small. Using a brute force attack method, one could easily try all (25) possible combinations to decrypt the message without initially knowing the key.
- The structure of the original plaintext remains intact. This makes the encryption method vulnerable to frequency analysis – by looking at h ow often certain characters or sequences of characters appear, one can discover patterns and potentially discover the key without having to perform a full brute force search.
The Caesar Cipher can be expressed in a more mathematical form as follows:
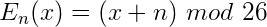
In plain terms, this means that the encryption of a letter x is equal to a shift of x + n, where n is the number of letters shifted. The result of the process is then taken under modulo division, essentially meaning that if a letter is shifted past the end of the alphabet, it wraps around to the beginning.
Decryption of the encrypted text (called the ciphertext) would be carried out similarly, subtracting the shift amount.
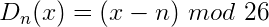
First used by Julius Caesar, the Caesar Cipher is one of the more well-known older historical encryption methods. While you certainly wouldn’t want to use it in today’s modern world, a long time ago it might have done the trick.
You can test out the Caesar Cipher using our Caesar Cipher Encryption tool. To learn more about digital security please take a look at the best VPN services in Canada.



